L'ASSONOMETRIA E LA QUOTATURA

Generalità

Come abbiamo detto, l'assonometria si basa sul presupposto che l'osservatore sia collocato all'infinito in modo che i raggi visuali provenienti dal suo occhio siano tutti paralleli fra loro. La direzione dei raggi proiettanti può essere obliqua oppure ortogonale al quadro ir. Di conseguenza l'assonometria si distingue in ortogonale e obliqua. La differenza fra i due tipi sta nel fatto che, mentre nell'assonometria obliqua il piano ir può essere assunto parallelo o coincidente con uno dei piani cartesiani di riferimento, nell'assonometria ortogonale questa circostanza deve essere esclusa, altrimenti il disegno, anziché un'assonometria, sarà ancora una proiezione ortogonale.

L'assonometria obliqua

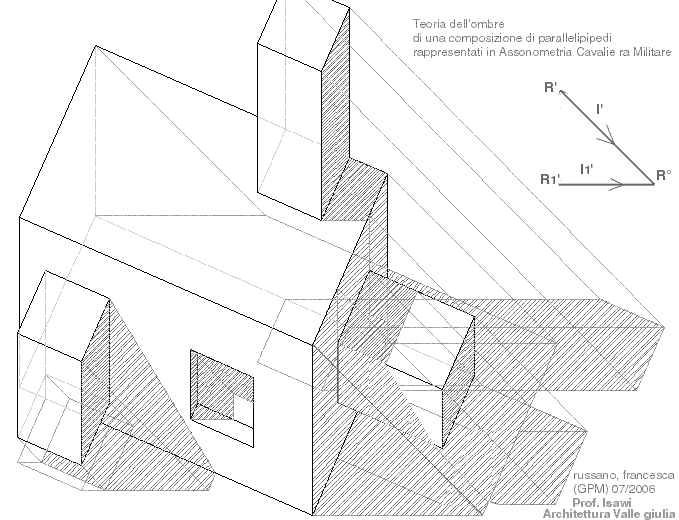
L'assonometria obliqua è di esecuzione molto più semplice e immediata dell'assonometria ortogonale, proprio perché è possibile far coincidere il quadro ir con uno dei piani cartesiani di riferimento. Quando si fa coincidere ir con il P.V., l'assonometria viene detta cavaliera; quando invece si fa coincidere TT col P.O., l'assonometria viene detta cavaliera militare o rapida.

L'assonometria cavaliera

Facciamo coincidere il quadro ir col P.V.; così anche gli assi x e z saranno coincidenti con questo piano e l'asse y lo toccherà già nel punto O. Basterà quindi proiettare su ir un qualsiasi altro punto A di y conducendo il raggio r inclinato secondo la direzione che abbiamo prescelto e che può essere qualunque purché obliqua al quadro. Il raggio r incontra ir in A; congiungendo O con A avremo la proiezione dell'intero asse y.Facciamo ora una considerazione. Gli assi cartesiani rappresentano le tre direzioni di larghezza, profondità e altezza, e su di essi si riportano le scale metriche relative a queste direzioni o le varie misure delle figure che si vogliono disegnare in assonometria; facendo coincidere il TT col P.V., x e z rimangono invariati e, con loro, anche le relative unità di misura assonometriche. Le unità di misura assonometriche relative ad y sono invece subordinate all'inclinazione che abbiamo scelto per il raggio proiettante r. In rapporto con questa inclinazione le unità assonometriche su y potranno essere maggiori, uguali o minori delle unità effettive. Nella pratica del disegno, sceglieremo di riportare su y le misure effettive, oppure di ridurle della' metà o di un terzo in base unicamente alla miglior resa visiva del nostro lavoro. Quando la nostra scelta cadrà sul rapporto 1:1:1,ossia quando sceglieremo di riportare le misure effettive anche su y, diremo che l'assonometria è monometrica. In questo caso però si percepisce immediatamente uno spiacevole allungamento della figura che può essere eliminato appunto riportando su y le misure ridotte della metà o di un terzo. Sempre in relazione all'inclinazione che abbiamo scelto per il raggio proiettante r, l'asse y potrà assumere diverse posizioni, che ci permetteranno di rappresentare gli oggetti come se li guardassimo dall' alto verso il basso dal basso verso l'alto, da sinistra verso destra, o da destra verso sinistra.

L'assonometria ortogonale

L'assonometria è ortogonale quando i raggi provenienti dall'infinito sono perpendicolari al quadro v. Per questo, come già abbiamo detto,, se non vogliamo ottenere ancora una proiezione ortogonale, dobbiamo mantenere il quadro obliquo ai piani cartesiani di riferimento e quindi obliquo agli assi. Un quadro obliquo agli assi li taglia secondo tre punti A,B,C, appartenenti rispettivamente a z,x,y. Congiungendo A con B, B con C, C con A, si ottengono i segmenti AB, BC, CA che sono le tracce del piano su P.V., P.O. e P.L La porzione del piano TT così limitata è sempre un triangolo acutangolo e viene detta triangolo fondamentale e assunta come piano dell'assonometria. il raggio proiettante passante per O, taglia ir in O che è l'assonometria di O. Congiungendo O con A,B e C otteniamo l'assonometria dei tre assi x,y,z che formano tra loro gli angoli AOB, AOC e BOC.

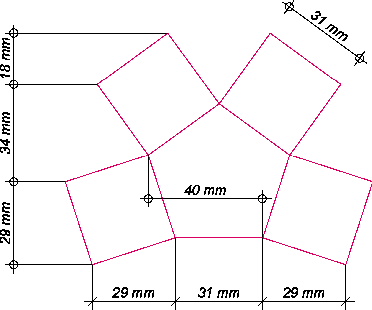
La quotatura

Indica, nel disegno tecnico, le informazioni dimensionali delle parti notevoli di un oggetto geometrico K, come lunghezza, larghezza, altezza, area, volume. Nella maggior parte dei casi gli oggetti quotati sono rappresentati con il metodo di Monge. la quotatura di una linea AB, eventualmente curva, è formata dai seguenti elementi: Linea di misura: linea parallela alla linea oggettiva A1B1. al centro del quale vien posto un valore numerico corrispondente alla lnghezza di AB.Linee di riferimento: linee terminate con frecce, delimitate dalle linee AB e con direzione normale a quest'ultime. Norme della quotatura Una volta ottenuta, ad esempio, una prima proiezione ortogonale di un oggetto K, si procede ad eseguirvi la quotatura rispettando le norme seguenti: Le linee di misura vanno poste esternamente rispetto alla proiezione di K.Le linee di misura devono riferirsi alle proiezioni di K che risultano in vera forma e non quelle deformate. Per esempio quando un spigolo di K è parallelo al piano di quadro, la sua proiezione risulta in vera misura, altrimenti ridotta, cioè, quando tale spigolo è inclinata rispetto al quadro.Gli assi di simmetria e le linee di proiezione di K non devono essere usate come linee di riferimento.Le linee di riferimento, le linee di misura e le frecce terminali non devono, quanto possibile attraversare le linee di proiezione.Le linee di misura, in caso di simmetria, possono essere interrotte dopo aver sorpassato di poco l'asse di simmetria. Se tali linee di misura sono numerose, esse possono essere anche sfalsate rispetto a tale asse. in tal caso le quote vanno scritte vicino alla unica freccia terminale di ciascuna linea di misura. Le linee di misura, in mancanza di spazio, possono essere prolungate esternamente e possibilmente a destra rispetto alle rispettive frecce.Le linee di misura devono essere parallele alle relative proiezioni di K. Per cui quando le proiezioni sono curve, ne consegue che, anche le linee di misure sono curve e sono omotetiche a tali proiezioni. Quando la curva è un arco di circonferenza la linea di misure del raggio va direzionata verso il centro di tale arco e con una sola freccia puntata su di esso. la quotatura del diametro di una circonferenza va posta possibilemente, su una linea orizzontale esterna rispetto a tale circonferenza e possibilmente orizzontale, Oppure passante per il centro ed inclinata di 30° rispetto al diametro orizzontale della stessa circonferenza.Tipi di quotatura in serie o a catena, in essa ogni proiezione va quotata rispetto a quella precedente.Quotatura in parallelo, ogni proiezione va quotata rispetto ad un stesso origine.Quotatura progressiva, ogni proiezione va quotata su una stessa linea di misura e sommando quella precedente. In questo caso le quote vanno scritte in corrispondenza della rispettiva linea di riferimento.